了解 avl tree 自平衡二元搜尋樹

Home >> Blog >> 了解 avl tree 自平衡二元搜尋樹

執行完SEO一天的進度後，讓我們來聊聊 avl tree 自平衡二元搜尋樹。

了解 avl tree 自平衡二元搜尋樹

AVL 樹是一種自平衡二叉搜尋樹 (BST)，其中所有節點的左右子樹的高度差不能超過

作為 AVL 樹的示例樹

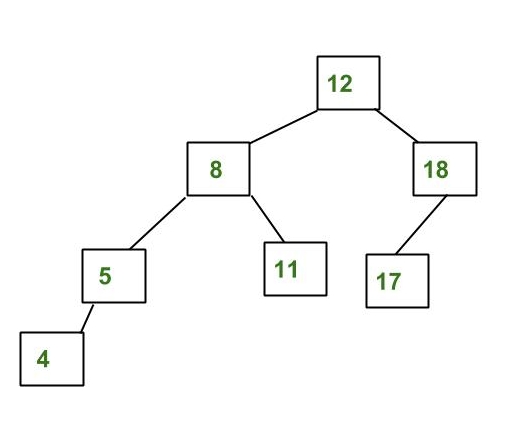
上面的樹是 AVL，因為每個節點的左右子樹的高度差小於或等於 1。不是 AVL 樹的示例樹

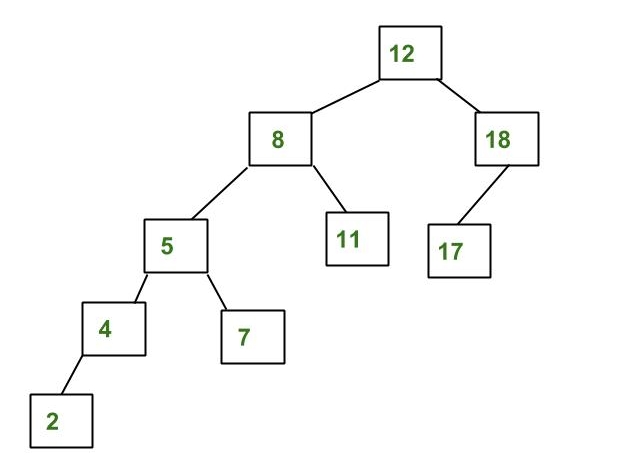
上面的樹不是 AVL，因為 8 和 12 的左右子樹的高度差大於 1。為什麼是 AVL 樹？大多數 BST 操作（例如，搜尋、最大值、最小值、插入、刪除……等）需要 O(h) 時間，其中 h 是 BST 的高度。對於傾斜的二叉樹，這些操作的成本可能會變成 O(n)。如果我們確保每次插入和刪除後樹的高度保持 O(Logn)，那麼我們可以保證所有這些操作的上限為 O(Logn)。AVL 樹的高度始終為 O(Logn)，其中 n 是樹中的節點數（有關證明，請參見此視頻講座）。

插入

為了確保給定的樹在每次插入後保持 AVL，我們必須增加標準 BST 插入操作以執行一些重新平衡。以下是在不違反 BST 屬性的情況下可以執行的兩個基本操作來重新平衡 BST（keys(left) < key(root) < keys(right)）。

1.左旋轉

2.右轉

T1、T2 和 T3 是樹的子樹
以 y （在左側）或 x （在
右側）
yx
/ \ 右旋轉 / \
x T3 - - - - - - - > T1 是
/ \ < - - - - - - - / \
T1 T2 左旋轉 T2 T3
上述兩棵樹中的鍵都遵循
以下順序
鍵（T1）<鍵（x）<鍵（T2）<鍵（y）<鍵（T3）
所以 BST 屬性在任何地方都沒有受到侵犯。

插入步驟

設新插入的節點為 w

對 w 執行標準 BST 插入。
從 w 開始，向上移動並找到第一個不平衡節點。設 z 是第一個不平衡節點，y 是 z 的子節點，它出現在從 w 到 z 的路徑上，x 是 z 的孫子節點，出現在從 w 到 z 的路徑上。
通過在以 z 為根的子樹上執行適當的旋轉來重新平衡樹。可能有 4 種可能的情況需要處理，因為 x、y 和 z 可以按 4 種方式排列。以下是可能的 4 種安排：

y 是 z 的左孩子，x 是 y 的左孩子（Left Left Case）
y 是 z 的左孩子，x 是 y 的右孩子（Left Right Case）
y 是 z 的右孩子，x 是 y 的右孩子（Right Right Case）
y 是 z 的右孩子，x 是 y 的左孩子（Right Left Case）

以下是上述 4 種情況下要執行的操作。在所有情況下，我們只需要重新平衡以 z 為根的子樹，整個樹就會變得平衡，因為以 z 為根的子樹（經過適當的旋轉）的高度與插入前相同。（見這個視頻講座的證明）

a) 左左大小寫

T1、T2、T3 和 T4 是子樹。
齊
/ \ / \
y T4 右旋轉 (z) xz
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2

b) 左右大小寫

zzx
/ \ / \ / \
y T4 左旋轉 (y) x T4 右旋轉 (z) yz
/ \ - - - - - - - - -> / \ - - - - - - - > / \ / \
T1 xy T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2

c) 右右大小寫

齊
/ \ / \
T1 y 左旋轉(z) zx
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4

d) 左右大小寫

zzx
/ \ / \ / \
T1 y 右旋轉 (y) T1 x 左旋轉 (z) zy
/ \ - - - - - - - - -> / \ - - - - - - - > / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4

插入示例：

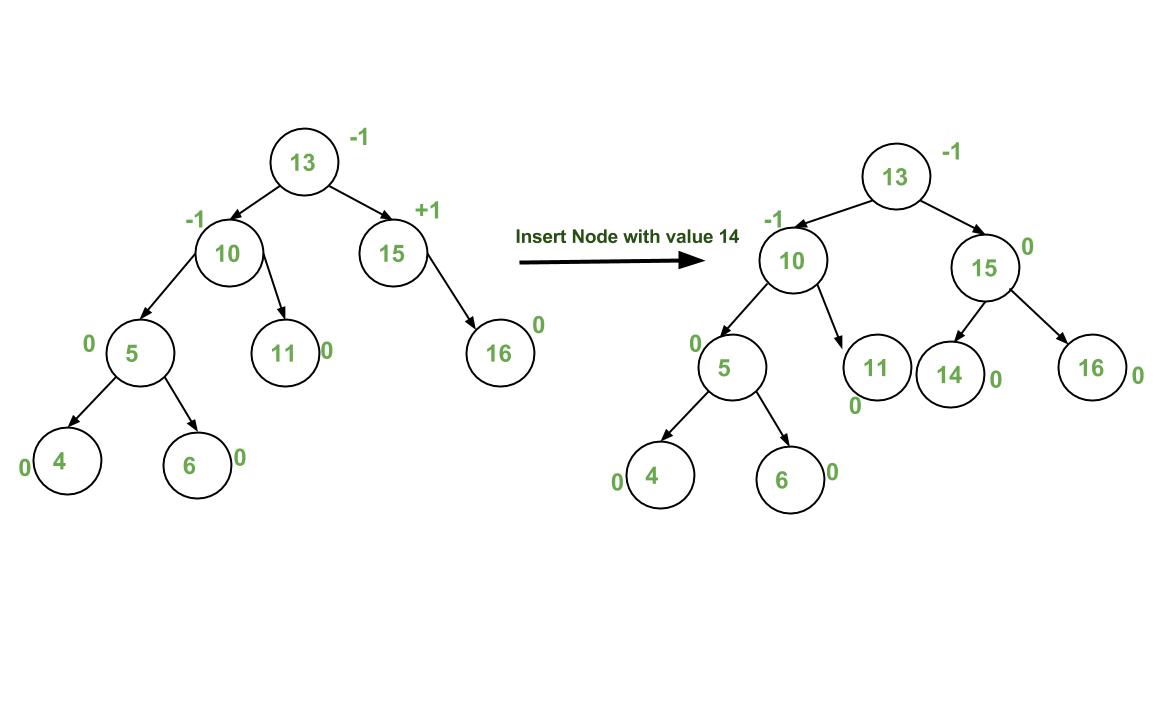
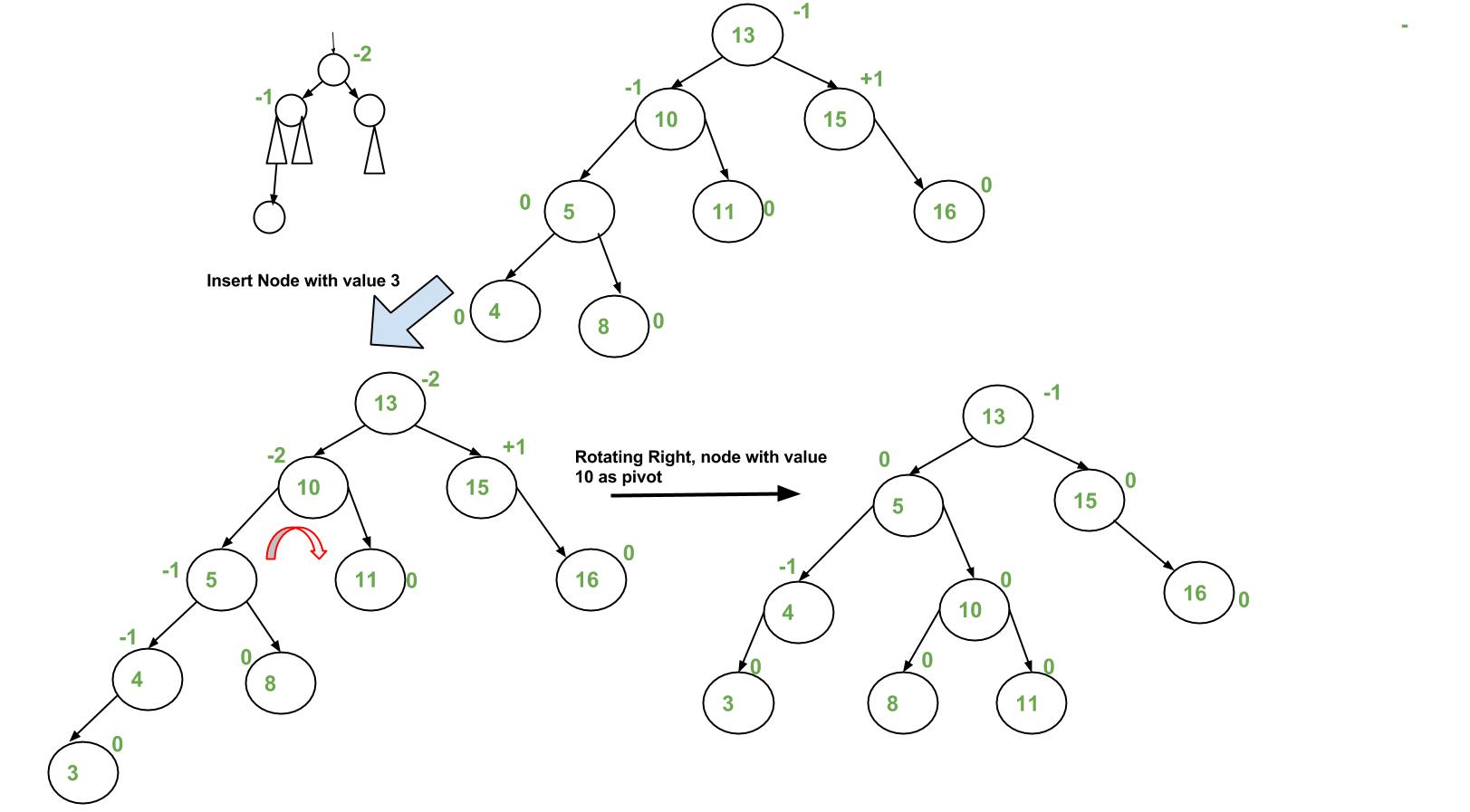
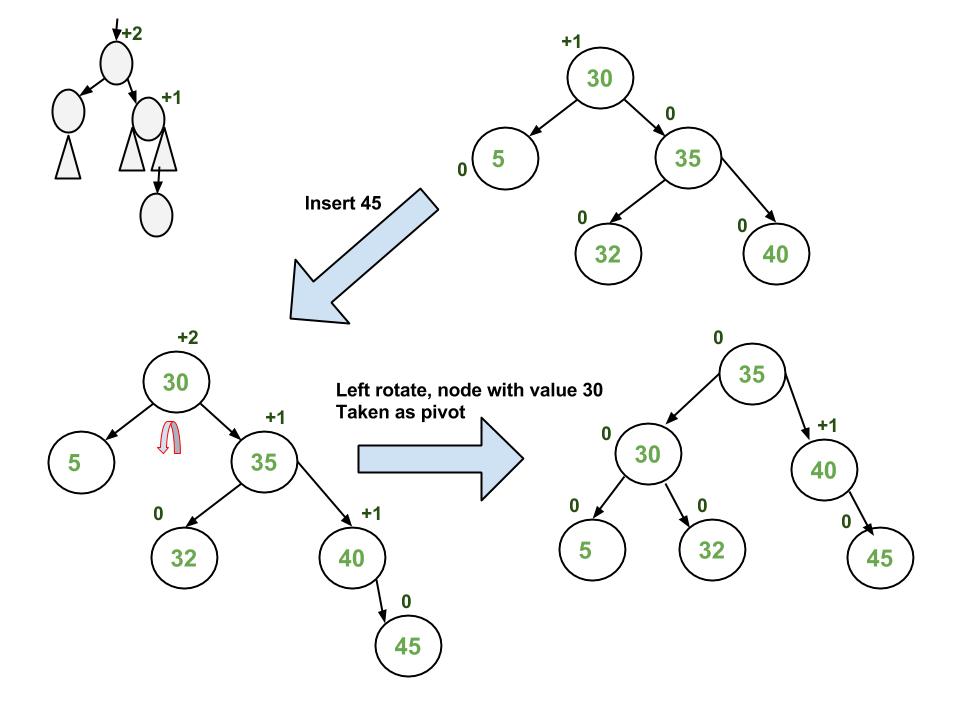
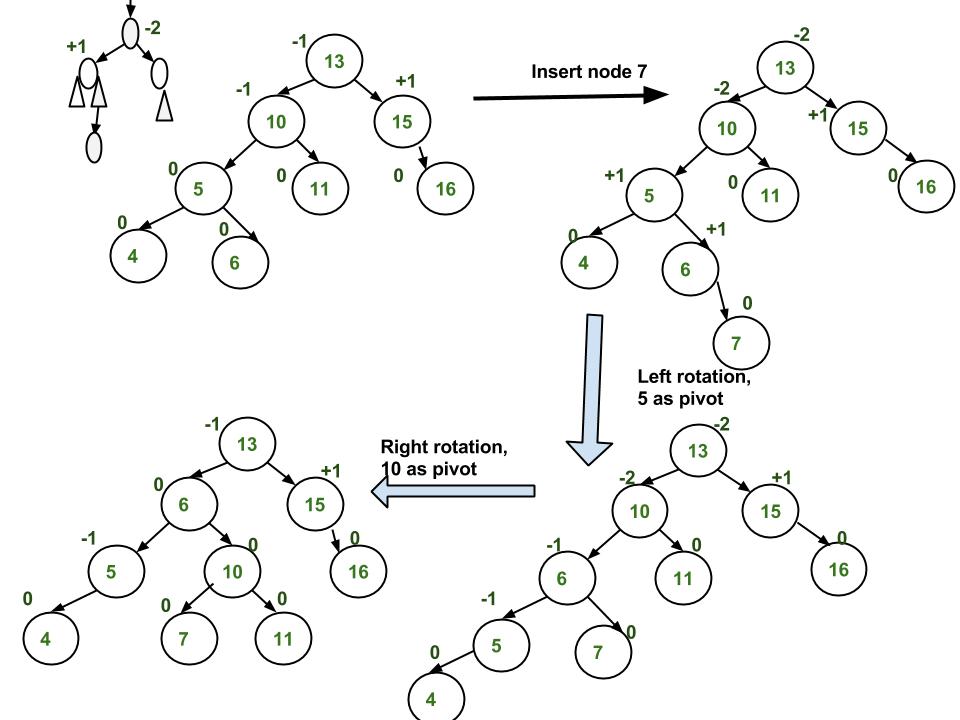
執行：

以下是 AVL 樹插入的實現。以下實現使用遞歸 BST 插入來插入新節點。在遞歸BST插入中，插入後，我們以自底向上的方式，一一獲取所有祖先的指針。所以我們不需要父指針向上移動。遞歸代碼本身向上傳播並訪問新插入節點的所有祖先。

執行正常的 BST 插入。
當前節點必須是新插入節點的祖先之一。更新當前節點的高度。
獲取當前節點的平衡因子（左子樹高度-右子樹高度）。
如果平衡因子大於 1，則當前節點是不平衡的，我們要么處於 Left Left 情況，要么處於 Left Right 情況。要檢查它是否是左左大小寫，請將新插入的鍵與左子樹根中的鍵進行比較。
如果平衡因子小於-1，則當前節點不平衡，我們處於右右情況或右左情況。要檢查它是否是右右大小寫，請將新插入的鍵與右子樹根中的鍵進行比較。

// C++ program to insert a node in AVL tree
#include< bits/stdc++.h>
using namespace std;

// An AVL tree node
class Node
{
public:
int key;
Node *left;
Node *right;
int height;
};

// A utility function to get maximum
// of two integers
int max(int a, int b);

// A utility function to get the
// height of the tree
int height(Node *N)
{
if (N == NULL)
return 0;
return N->height;
}

// A utility function to get maximum
// of two integers
int max(int a, int b)
{
return (a > b)? a : b;
}

/* Helper function that allocates a
new node with the given key and
NULL left and right pointers. */
Node* newNode(int key)
{
Node* node = new Node();
node->key = key;
node->left = NULL;
node->right = NULL;
node->height = 1; // new node is initially
// added at leaf
return(node);
}

// A utility function to right
// rotate subtree rooted with y
// See the diagram given above.
Node *rightRotate(Node *y)
{
Node *x = y->left;
Node *T2 = x->right;

// Perform rotation
x->right = y;
y->left = T2;

// Update heights
y->height = max(height(y->left),
height(y->right)) + 1;
x->height = max(height(x->left),
height(x->right)) + 1;

// Return new root
return x;
}

// A utility function to left
// rotate subtree rooted with x
// See the diagram given above.
Node *leftRotate(Node *x)
{
Node *y = x->right;
Node *T2 = y->left;

// Perform rotation
y->left = x;
x->right = T2;

// Update heights
x->height = max(height(x->left),
height(x->right)) + 1;
y->height = max(height(y->left),
height(y->right)) + 1;

// Return new root
return y;
}
// Get Balance factor of node N
int getBalance(Node *N)
{
if (N == NULL)
return 0;
return height(N->left) - height(N->right);
}
// Recursive function to insert a key
// in the subtree rooted with node and
// returns the new root of the subtree.
Node* insert(Node* node, int key)
{
/* 1. Perform the normal BST insertion */
if (node == NULL)
return(newNode(key));

if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
else // Equal keys are not allowed in BST
return node;

/* 2. Update height of this ancestor node */
node->height = 1 + max(height(node->left),
height(node->right));

/* 3. Get the balance factor of this ancestor
node to check whether this node became
unbalanced */
int balance = getBalance(node);

// If this node becomes unbalanced, then
// there are 4 cases

// Left Left Case
if (balance > 1 && key < node->left->key)
return rightRotate(node);

// Right Right Case
if (balance < -1 && key > node->right->key)
return leftRotate(node);

// Left Right Case
if (balance > 1 && key > node->left->key)
{
node->left = leftRotate(node->left);
return rightRotate(node);
}

// Right Left Case
if (balance < -1 && key < node->right->key)
{
node->right = rightRotate(node->right);
return leftRotate(node);
}
/* return the (unchanged) node pointer */
return node;
}

// A utility function to print preorder
// traversal of the tree.
// The function also prints height
// of every node
void preOrder(Node *root)
{
if(root != NULL)
{
cout << root->key << " ";

preOrder(root->left);
preOrder(root->right);
}
}

// Driver Code
int main()
{
Node *root = NULL;

/* Constructing tree given in
the above figure */
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
root = insert(root, 50);
root = insert(root, 25);

/* The constructed AVL Tree would be
30
/ \
20 40
/ \ \
10 25 50
*/
cout << "Preorder traversal of the "
"constructed AVL tree is \n";
preOrder(root);

return 0;
}

// This code is contributed by
// rathbhupendra

輸出：

構建的 AVL 樹的前序遍歷為
30 20 10 25 40 50

時間複雜度：旋轉操作（左旋轉和右旋轉）需要恆定的時間，因為那裡只有幾個指針被改變。更新高度和獲取平衡因子也需要一定的時間。因此 AVL 插入的時間複雜度與 BST 插入的時間複雜度相同，即 O(h)，其中 h 是樹的高度。由於 AVL 樹是平衡的，因此高度為 O(Logn)。所以 AVL 插入的時間複雜度是 O(Logn)。

與紅黑樹

的比較：AVL 樹和其他自平衡搜尋樹（如紅黑）對於在 O(log n) 時間內完成所有基本操作很有用。與紅黑樹相比，AVL 樹更平衡，但它們在插入和刪除過程中可能會導致更多的旋轉。因此，如果您的應用程序涉及許多頻繁的插入和刪除，那麼應該首選紅黑樹。如果插入和刪除不那麼頻繁，而搜尋是更頻繁的操作，那麼 AVL 樹應該優先於紅黑樹。以下是刪除的帖子。

了解 avl tree 自平衡二元搜尋樹